Leetcode-721题解

leetcode 721 题解
并查集简介

题目

给定一个列表 accounts，每个元素 accounts[i] 是一个字符串列表，其中第一个元素 accounts[i][0] 是 名称 (name)，其余元素是 emails 表示该账户的邮箱地址。

现在，我们想合并这些账户。如果两个账户都有一些共同的邮箱地址，则两个账户必定属于同一个人。请注意，即使两个账户具有相同的名称，它们也可能属于不同的人，因为人们可能具有相同的名称。一个人最初可以拥有任意数量的账户，但其所有账户都具有相同的名称。

合并账户后，按以下格式返回账户：每个账户的第一个元素是名称，其余元素是 按字符 ASCII 顺序排列 的邮箱地址。账户本身可以以 任意顺序 返回。

示例 1：
输入：accounts = [[“John”, “johnsmith@mail.com“, “john00@mail.com“], [“John”, “johnnybravo@mail.com“], [“John”, “johnsmith@mail.com“, “john_newyork@mail.com“], [“Mary”, “mary@mail.com“]]
输出：[[“John”, ‘john00@mail.com‘, ‘john_newyork@mail.com‘, ‘johnsmith@mail.com‘], [“John”, “johnnybravo@mail.com“], [“Mary”, “mary@mail.com“]]
解释：
第一个和第三个 John 是同一个人，因为他们有共同的邮箱地址 “johnsmith@mail.com“。
第二个 John 和 Mary 是不同的人，因为他们的邮箱地址没有被其他帐户使用。
可以以任何顺序返回这些列表，例如答案 [[‘Mary’，‘mary@mail.com‘]，[‘John’，‘johnnybravo@mail.com‘]，
[‘John’，‘john00@mail.com‘，‘john_newyork@mail.com‘，‘johnsmith@mail.com‘]] 也是正确的。

示例 2：
输入：accounts = [[“Gabe”,”Gabe0@m.co“,”Gabe3@m.co“,”Gabe1@m.co“],[“Kevin”,”Kevin3@m.co“,”Kevin5@m.co“,”Kevin0@m.co“],[“Ethan”,”Ethan5@m.co“,”Ethan4@m.co“,”Ethan0@m.co“],[“Hanzo”,”Hanzo3@m.co“,”Hanzo1@m.co“,”Hanzo0@m.co“],[“Fern”,”Fern5@m.co“,”Fern1@m.co“,”Fern0@m.co“]]
输出：[[“Ethan”,”Ethan0@m.co“,”Ethan4@m.co“,”Ethan5@m.co“],[“Gabe”,”Gabe0@m.co“,”Gabe1@m.co“,”Gabe3@m.co“],[“Hanzo”,”Hanzo0@m.co“,”Hanzo1@m.co“,”Hanzo3@m.co“],[“Kevin”,”Kevin0@m.co“,”Kevin3@m.co“,”Kevin5@m.co“],[“Fern”,”Fern0@m.co“,”Fern1@m.co“,”Fern5@m.co“]]

提示：
1 <= accounts.length <= 1000
2 <= accounts[i].length <= 10
1 <= accounts[i][j].length <= 30
accounts[i][0] 由英文字母组成
accounts[i][j] (for j > 0) 是有效的邮箱地址

思路

并查集+哈希表

此题的难点在于判断邮箱是否属于同一个人，而并查集可以很方便的做到这一点。并查集简介：

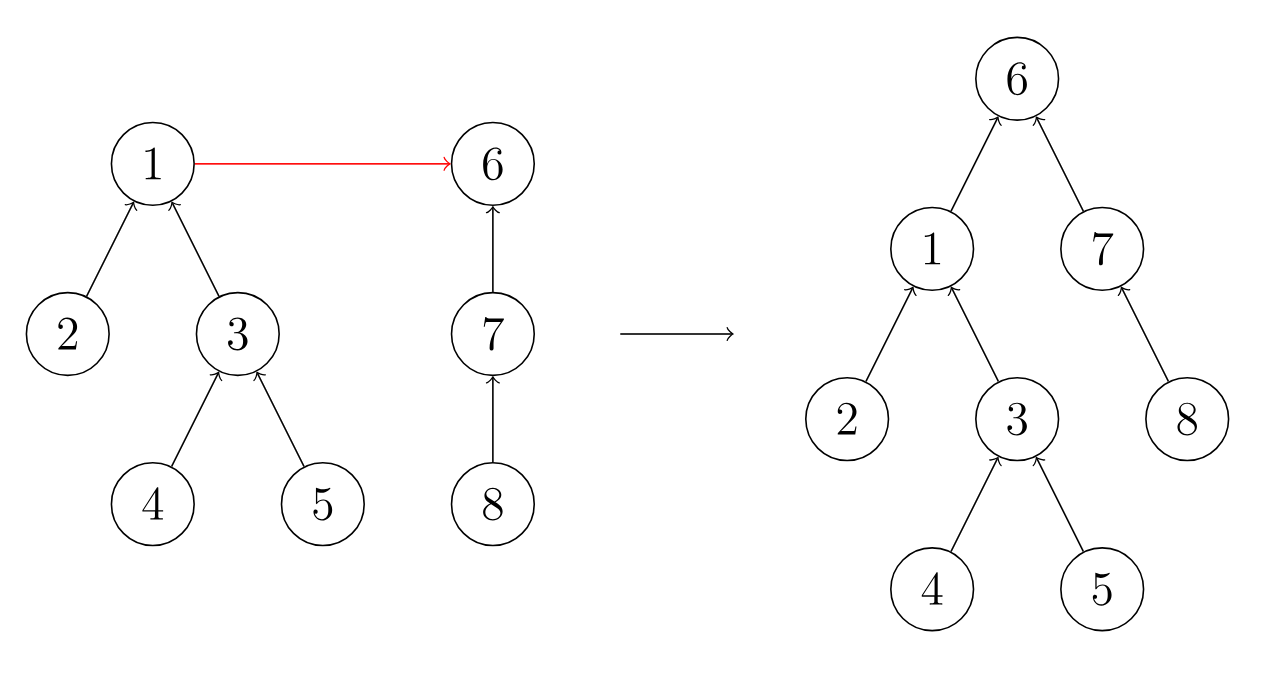
并查集可以理解为一个森林，每棵树表示为一个集合，树中的节点表示对应集合中的元素，不同集合的元素指向不同的根。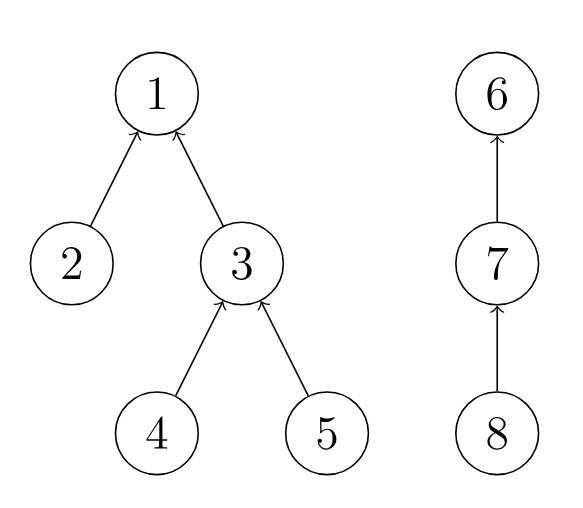

顾名思义，并查集支持合并和查找。使用数组表示并查集，数组中记录的是每个节点对应的根节点（的编号）。

1. 用类封装并查集

   1 2 3 4

   class unionSet { public: vector<int> nums; };

2. 初始化
   将所有节点的根设置为它自己。 resize 是调整数组的大小。

   1 2 3 4 5 6

   unionSet(int n) { nums.resize(n); for (int i = 0; i < n; i++) { nums[i] = i; } }

3. 合并函数
   将节点2的根节点设为节点1的根节点。
   

   1 2 3 4

   void set(int index1, int index2) { parent[find(index2)] = find(index1); return; }

4. 查找函数
   递归查找当前节点对应的根节点，直到当前节点的下标与根节点一致。

   1 2 3

   int find(int index) { return parent[index] == index ? index : find(parent[index]); }

介绍完并查集，使用并查集来解决本题。本题的思路就是，将 每个邮箱 映射为一个数字，然后在该数字的基础上使用并查集的思想合并同一个人的邮箱，最后把同一个人的邮箱进行排序，然后返回结果。所以，第一步需要将邮箱映射到数字和名字，然后使用并查集合并同一个人的邮箱。

然后就是本题中相对复杂的一部分，将同一个人的所有邮箱找出来。因为在上一步中，我们已经合并了同一个人的邮箱。所以在这一步中，我们遍历邮箱到数字的哈希表（每个相同的邮箱只会出现一次，并且有相同的 id ）。使用一个哈希表记录每个人对应的邮箱（用vector数组表示），键可以是任意的，只要每个相同的人对应的键是相同的即可。所以，我们使用每个邮箱在哈希表中的根作为键，这样就保证了每个人的键的唯一性。根据这个键查找并加入邮箱。这一步完成后，我们就得到了一个哈希表，键是数字（每个人唯一），值是包含所有邮箱的数组。

最后一步就是把邮箱和名字对应起来，并对邮箱进行排序。我们可以直接使用 sort() 函数对 vector 数组中的邮箱进行排序，然后根据第一步中的哈希表（邮箱到名字）找到名字，最后得到结果并返回。

时间复杂度应该是 $O(n \log n)$ 。其中 $n$ 是不同邮箱地址的数量。
需要遍历所有邮箱地址，在并查集内进行查找和合并操作，对于两个不同的邮箱地址，如果它们的祖先不同则需要进行合并，需要进行 2 次查找和最多 1 次合并。一共需要进行 $2n$ 次查找和最多 $n$ 次合并，因此时间复杂度是 $O(2n \log n)=O(n \log n)$ 。
整理出题目要求的返回账户的格式时需要对邮箱地址排序，时间复杂度是 $O(n \log n)$ 。
其余操作包括遍历所有邮箱地址，在哈希表中记录相应的信息，时间复杂度是 $O(n)$ ，在渐进意义下 $O(n)$ 小于 $O(n \log n)$ 。
因此总时间复杂度是 $O(n \log n)$ 。

空间复杂度是 $O(n)$ ，其中 $n$ 是不同邮箱地址的数量。空间复杂度主要取决于哈希表和并查集，每个哈希表存储的邮箱地址的数量为 $n$ ，并查集的大小为 $n$ 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

class unionSet {
public:
    vector<int> parent;
    unionSet(int n) {
        parent.resize(n);
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }

    void set(int index1, int index2) {
        parent[find(index2)] = find(index1);
        return;
    }

    int find(int index) {
        return parent[index] == index ? index : find(parent[index]);
    }
};

class Solution {
public:
    vector<vector<string>> accountsMerge(vector<vector<string>>& accounts) {
        unordered_map<string, string> mailtoPeople;
        unordered_map<string, int> mailtoNum;
        unordered_map<int, vector<string>> numToMail;
        vector<vector<string>> result;
        int mailCount = 0;
        for (int i = 0; i < accounts.size(); i++) {
            for (int j = 1; j < accounts[i].size(); j++) {
                if (!mailtoPeople.count(accounts[i][j])) {
                    mailtoPeople[accounts[i][j]] = accounts[i][0];
                    mailtoNum[accounts[i][j]] = mailCount;
                    mailCount++;
                }
            }
        }
        unionSet unionset(mailCount);
        for (int i = 0; i < accounts.size(); i++) {
            string firstMail = accounts[i][1];
            int firstIndex = mailtoNum[firstMail];
            for (int j = 2; j < accounts[i].size(); j++) {
                string nextMail = accounts[i][j];
                int nextIndex = mailtoNum[nextMail];
                unionset.set(firstIndex, nextIndex);
            }
        }
        for (auto& [mail, _] : mailtoNum) {
            int index = unionset.find(mailtoNum[mail]);
            vector<string>& account = numToMail[index];
            account.push_back(mail);
            numToMail[index] = account;
        }
        for (auto& [num, mail] : numToMail) {
            sort(mail.begin(), mail.end());
            vector<string> tempresult;
            tempresult.push_back(mailtoPeople[mail[0]]);
            for (auto& eachmail : mail) {
                tempresult.push_back(eachmail);
            }
            result.push_back(tempresult);
        }
        return result;
    }
};